Unit 5 九章高级算法课: 动态规划
标签(空格分隔): leetcode DP 九章
Overview
- 空间优化
- 记忆化搜索
- 循环引用的状态数组
- 区间动态规划
动态规划4要素
- 状态 State
- 灵感, 创造力, 储存小规模问题的结果 a. 最优解/max/min b. Yes/No c. count(*)
- 方程 Recurrance function
- 状态之间的联系, 怎么通过小的状态来求得大的状态
- 初始化 Initialization
- 最极限的小状态是什么: 起点
- 答案 Answer
- 最大的状态是什么: 终点
空间优化
House Robber
有2种DP定义
- P[i]: 前i个房子, 包括或不包括的最大价值. 这个是Stanford algs讲的WIS的思想, 也是01背包的讲法. 大问题拆成2个小问题.
- P[i]: 偷了前i个房子, 包括第i个房子的, 最大价值. 这个方法的终点不是ans, 而要对所有P[i]求最大. 因为偷了最后一个房子得到的最大价值并不一定就是最大值. 例子就是题目给的example: [3,8,4]. 最大是8. 即P[1].
先看我的写法:
P[i] = Max{P[i-2]+A[i], P[i-1]}. 那么解就是P[A.length-1].- 但是空间就是O(N)了. 其实可以优化到O(1).
- 田老师讲了:
蓝色的风@Pue 11/10/15 9:32:08 PM 如果只有三个状态那是可以mod 3, 四个状态就mod 4.
因为P[i]只和2个子状态有关. 所以一共是3个状态. 那就是大小为3的P即可. 我一开始写成了4也可以. 然后试了大于3的mod都可以. 看来取模真是牛.
- 但是要想想为什么可以. 取模是压缩了数组. 例如:P[3]~((P[0],P[1])有关. 则取模后: P[0]~(P[0], P[1]). 所以覆盖了也没问题.
- 还想了是不是P[a]~(P[a-123], P[a-567])也是取模3, 用大小为3的数组. 我想还是对的. 但是没想到举个什么例子.
- 所以暂且记住: recurrence function里有几个状态就模几.
总之, 我改成
P[i%3] = Math.max(P[(i-2)%3] + A[i], P[(i - 1)%3]);就OK了.但是原本的解就不在哪个位置了, 所以return max(P[0], P[1], P[2]).. 真傻, 当然是确定的, 就是P[A.length % 3].
然后是九章的解法
- 定义P[i]为: 前i个房子中, 偷了第i个房子的最大价值. 这里的方程有意思: max(P[i-2], P[i-3])+A[i]. 为什么呢? 这里有一点证明. 看视频里有讲. 这里等我有空写一下. 所以有了模版也不一定做得出来, 要想出来其中的数学关系. 同理参考为什么trapping water I/II用minPQ.
- 一开始我也是想着最后的话, ans是P[]中最大的那个, 因为偷了i房子的最大价值并不一定是全局最大. 当然了, loop一遍找最大当然是ans. 但是想想: 最大只有可能是P[A.length-2], P[A.length-1]中的一个. 因为当k<A.length-2. P[k]当然小于P[k]+A[A.length-1]. 就这么一句话证明, 就从O(n)变为O(2)即O(1). 所以题目的条件要思考!
Maximum Square
即给一个matrix of 01. 找到最大的正方形岛屿. 1是陆地, 0是海洋.
- DP问题的关键是找到recurrence function. 所以才会有Leetcode动归总结, 动归公式合集 这题想到了公式就解决了.
- 公式怎么想? 当然是先用brute force. 然后再说, 一上来如果没有DP思路的话应该先通过brute force做, 从而找到思路, 于是有了规律. 也就好想了. 九章老师也是这么开始讲解的.
思路1
- 对于每一个(i,j), 将他作为左上角, 如果为1,
那么就可以向(i+1, j), (i, j+1), 和(i+1, j+1)走. 如果这3个点都为1.然后再...应该是. 对于每一个点, 如果为1. for len : 1 to n.的尝试. 伪代码
for (int i = 0; i < R; ++i) { for (int j = 0; j < C; ++j) { for (int len = 1; len < min(R,C); ++len) { if (点(i,j)为左上角, 边长为len的空间是正方形) { ans = max(ans, len); } } } } return ans * ans;这个复杂度是: $$O(RClen*len)$$. 即O(n^4).
思路2
- 对于每一个点(i,j). 将他作为右下角. 那么如图所示, 红方块即(i,j), 其值为1. 以它的3个锚点向上找, 假定已经各自找到了最大的正方形: 有3个正方形: 绿色的以(i-1,j)为右下角. 紫色以(i-1,j-1)为右下角, 咖啡色以(i,j-1)为右下角. 那么加上(i,j). 可以得到的最大正方形是什么呢? 显然(这里思考一下). 是用最小的正方形: 咖啡色扩充到1的正方形.
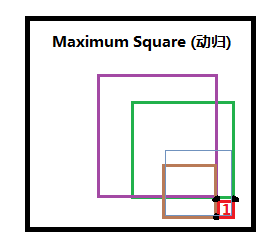 .
. - 那么这里就要求到达(i,j)点已经知道了以周围3个锚点为右下角所组成的最大正方形-> 即动态规划.
- 于是得到了recurrence function: 定义P[i][j]表示以(i,j)为右下角的最大正方形的边长. 于是按照上面的思路: P[i][j] = min(P[i-1][j], P[i][j-1], P[i-1][j-1])+1.
拓展一下: 求最大矩形岛屿.
- 其实这个时候思路一样, 但是由于没有了正方形的限制: 长宽一样大. 那么可以找长/宽中最长的即可.
- 也就是说刚才用P[i][j]表示当前点为右下角的最大边长, 现在要用2个DP表: W[i][j]和H[i][j]. 表示当前点为右下角的最大Width和最大Height. 但是我没想出来这个recurrence function.
- 学得技能: 要往做过的题目靠. 经典数据结构和算法要熟练. 图形分析也很重要.
解法1: O(n^2)时间, O(n)空间(用lichen博客下面tia的comment)
记得之前做过的Stack经典题目吗: largest rectangle in histogram. 这里不是一样吗? 见李二娃的博客, 以及他的图示:
 .
.- 分析: 可以把每一层转化为一个histogram.(从0层到该层组成的histogram). 然后用O(n)的largest rectangle in histogram即可. 所以总共是O(n^2)
不过不要忘了怎么写的largest rectangle in histogram. 应该从brute force开始推. 然后想到stack. 然后想到是处理完(pop完)比curHeight小的index. 然后再插入.
- 于是想到了sliding window, 和median. 即: 先入再出, 还是先出再入?
- 有个index的细节. 即若: i也是右边界, 那么width: i-j+1. 如果i是右边界的下一个, 那么width: i-j. 但是这里为什么是: i-stk.peek()-1呢? 因为i是右边界. 左边界是比当前bar小的bar. 因为我们就是用的单增stack, 就是peek()即可. 见下图:
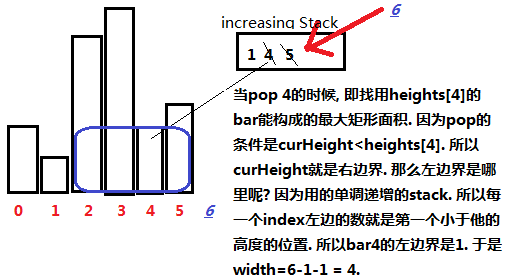
- 为什么这里是先pop, 再push. 而sliding windows maximum是先add, 在remove?
- Ans: loop的目的是保证container的invarient! invariant! invariant! 重要的事情说三遍! 同理参见<九章高算的Two pointer>: maximum Subarray contains target string中while loop
- 为什么是
<=? 因为单调递增stack, 即stack中的数的左边的数就是他左边比他小的第一个高度的index.
代码如下:
private int maxRecHist(int[] heights) { int ans = 0; Stack<Integer> incStk = new Stack<>(); for (int i = 0; i <= heights.length; ++i) { int curHeight = i == heights.length? 0 : heights[i]; while(!incStk.isEmpty() && curHeights <= heights[incStk.peek()]) { // 为什么<=? int idxH = heights.pop(); int width; if (incStk.isEmpty()) { width = i; } else { width = i - incStk.peek() - 1; // Key point of using the increasing stack. } ans = Math.max(ans, width * heights[idxH]); } incStk.push(i); // 为什么这里是先pop后push呢? } return ans; }
解法2 Leetcode答案
- 使用DP. 不过挺不错. 用了3个DP表: left[i,j], right[i,j], height[i,j].
- 记得以前也见过一道DP题目, 也是用了2个DP表就很好做了. 是哪题? Ans: 想起来了, 是maximum product array. 即保存2个DP[]: min[], max[].
- 有空细看一下, 刚才跑了一下, 感觉结果有点问题.
记忆化搜索
DP有2个类型的求值:
- 常见的for loop : i = 1 ~ n.
- 记忆化搜索: skii, triangle, etc.
- 记忆化搜索一般是因为简单的iteration 的 for loop不好找每一个状态的结果. 也许会有互相依赖的情况, 那么就导致了死循环. 例如skii的recurrence function如下, $$f(i,j) = Max[f(i-1, j), f(i,j-1), f(i+1,j), f(i,j+1)] + 1$$那么f(i,j-1)又会依赖到
f(i,j), f(i-1,j-1)$$f(i,j-1) = Max[f(i-1, j-1), f(i,j-2), f(i+1,j-1), f(i,j)] + 1$$. 于是有了记忆化搜索的动态规划. 一般是递推的形式. 但是注意: 递推只是形式! 和普通的递推不一样!!! 参考triangle的记忆化搜索和递推, 2个解法的区别.
原来我搞混了backtracking, 递归, 记忆化搜索: 递归是代码的组合形式, 和算法无关. backtracking和记忆化搜索是2种算法. 前者是在所有子集里面找符合条件的解集, 后者则是当DP的状态不好递推求解的时候, 使用记忆化, 则计算过的不用考虑.算法竞赛入门经典完整版VS挑战程序设计竞赛都已经解释了各自的区别. 在backtracking中, 之所以要恢复状态(全局辅助变量)是因为那个状态的解已经求出. 而要求下一个解, 那么辅助变量就要恢复到新的状态的初始值. 总之就是2个是不相干的算法, 只是都用recursion来写而已.- 刘如佳讲过了, 贴个图, 以triangle为例:
, 于是推出了DP:
.
写一下记忆化搜索DP的模版: ``` int[] P = new int[size];
private int dfs(int i, int[] P, boolean[] visited) { if (visited[i]) { return P[i]; } int ans = 0; if (smallest state) { set smallest state; } else { // to update P[i], need other valid next states, for example: P[i-1], P[i+1]. for (valid next states) { update P[i] = f(dfs(i-1, P, visited), dfs(i+1, P, visited); // f() maybe max/min,... } } visited[i] = true; // 注意这里只要经过的, 就不用在重新计算了. 和backtracking不同! return P[i]; } ```
- 老师总结的很精辟:
- for iteration来得到P[][]是遍历i = 1~>n.
- 而记忆化搜索则是已知n, 然后从n~>1. 即大状态递推到小状态. (什么是大小状态?)
经典的记忆化搜索题目: 博弈类游戏: min-max tree的应用: coins in a line I/II/III
题目是: There are n coins in a line. Two players take turns to take one or two coins from right side until there are no more coins left. The player who take the last coin wins. Could you please decide the first play will win or lose?
即有一排coins: [1,3,2,20]. 每个人轮流从右侧一次拿1或2个coins. 谁拿到最后一个就是谁赢. 求先手是否必胜.
我一开始完全没有思路, 2个人跑, 而且每一步都不确定. 谁知道下一步应该拿1个还是2个?
- 所以老师说了: 对于这种不好用iteration的DP题目, 就反过来, 从n推到1. 即large state推到small state. 于是也就需要用recursion的形式. 那么递推式是怎样的呢? 怎么想? 其实空想当然不好想. 画图分析. (当然, 不是乱画图, 要学会每一题的思路, 然后遇到新的题目, 就自然有思路了).
- 老师定义了: DP[n]表示先手在面对n个coins的时候是否有必胜的可能性. 那么n->1, 那么小state怎么推呢?
- 如图所示: