Best Time to Buy and Sell Stock with Cooldown

  • medium
  • tag: DP
  • similar: BTBSS IV, 互相调用的DP

>

思路

idea 1: DP公式的思考过程

  • dietpepsi的discuss的链接

  • 先是通过2个要求:

    1. We have to rest before we buy and

    2. we have to buy before we `sell.

      得到了3个关系式:

      $$buy[i] = max(rest[i-1]-price, buy[i-1]) $$ $$sell[i] = max(buy[i-1]+price, sell[i-1])$$ $$rest[i] = max(sell[i-1], buy[i-1], rest[i-1])$$

  • 不过里面的2个further observation是通过logic推理出来的, 而不是公式. 而且这几个公式/推论的意义想了我一个早上!

    buy[i] <= rest[i] which means rest[i] = max(sell[i-1], rest[i-1]). That made sure [buy, rest, buy] is never occurred.

    • 这是怎么推出来的? 上面这个公式和[buy,rest,buy]不存在有什么关系? Ans: 因为到i为止, 以rest结尾的最大收益只和sell[i-1], rest[i-1]有关. 换句话说, rest[i]的最大收益是建立在i-1的sell, 然后i时刻rest, 或者rest[i-1]且i时刻rest. 故rest的话, 他前一时刻肯定是rest或者sell, 而不可能是buy! 所以不会出现: buy, rest. 而肯定是: sell, rest, rest, ..., rest, sell, rest, 或者是buy, rest, rest, ..., rest, rest.

  • 那么furthor observation: $$rest[i] \le sell[i]$$, 怎么得出来的呢? 我用上面的3个关系式得不出这个关系. 但是用logic很容易理解, 因为以sell结尾的肯定比rest结尾收益大????

    • 并不是: 5,4,3,2,1. sell[i]都为负数, 而rest[i]为0.

  • 代码如下:

public int maxProfit(int[] prices) {
    if (prices == null || prices.length < 2)  return 0;

    int[] buy = new int[2];
    int[] sell = new int[3];
    buy[0] = -prices[0];
    buy[1] = Math.max(-prices[0], -prices[1]);
    sell[0] = 0;
    sell[1] = Math.max(0, prices[1]-prices[0]);
    for (int i = 2; i < prices.length; ++i) {
      buy[i%2] = Math.max(sell[(i-2)%3]-prices[i], buy[(i-1)%2]);
      sell[i%3] = Math.max(buy[(i-1)%2]+prices[i], sell[(i-1)%3]);
    }
    return sell[(prices.length-1)%3];
}
  • 注意: 使用rolling array的时候, 有几个决策就用多大的state. 由于sell使用了i-2, i-1, i, 所以sell[3]. 而buy则是buy[2].

idea 2: DP the easiest Java solution

  • 虽然最高分的posts给了很多启发, 但是总有几个地方想不通.

  • 所以the easiest post反而容易想. 这次只需要2个array: buy[i]和sell[i]. 分别表示到第i天的最大收益, 前者的最后一步是buy,后者的最后一步是sell. 但都不一定是第i天行动. 即可以在0~i天做action, 剩余的天则rest. 也就是九章所说的state的2种表达的第二种:

    1. F[i]表示到第i天的最大利益, Action on ith day. (这种表达式比较常见, 因为好确定)
    2. F[i]表示到第i天的最大利益, May or maynot action on ith day. (这题使用的这种表述)

  • 递推公式:

    • buy[i]: 可以分解为2种情况, 第i天买或不买, 如果第i天买的话, 那就必须先卖出去, 由于卖之后必须rest, 但是不知道sell和buy之间有几个rest, 所以我们定义state的时候使用的第二种表述. 如果第i天不买的话, 要最大收益的话, 肯定是buy[i-1].

      1. buy @ ith day, sell[i-2] - prices[i].
      2. rest @ ith day, buy[i-1].

    • sell[i]: 可以分解为2种情况, 第i天sell或不sell. 若sell的话, 很简单, 就是buy[i-1]+prices[i]. 若不sell的话, 就必定是sell[i-1].

  • 以上的公式都是表示当前的收益, 所以第i天买的话, 需要-prices[i], 若sell的话, 则是+prices[i].

  • 然后我很喜欢yavinci 的O(1)空间优化的方法, 从var name到推导, 都很清晰明了.

    • 用b2,b1,b0表示buy[i-2], buy[i-1], buy[i].
    • 用s2,s1,s0表示sell[i-2], sell[i-1], sell[i].
    • 从而很简单的写出上面的公式:
      • b0 = Math.max(b1, s2-prices[i])
      • s0 = Math.max(b1+prices[i], s1)
      • b1 = b0; s2 = s1; s1 = s0; 注意s2,s1更新的顺序, 要使用旧的s1赋值给s2. 所以把s1的更新放到s2的后面.

  • 代码如下:

public int maxProfitEesiest(int[] prices) {
    if (prices == null || prices.length < 2)  return 0;
    int b0 = -prices[0], b1 = b0;
    int s0 = 0, s1 = 0, s2 = 0;  // why?

    for (int i = 1; i < prices.length; ++i) {
      b0 = Math.max(b1, s2-prices[i]);
      s0 = Math.max(s1, b1+prices[i]);
      b1 = b0; s2 = s1; s1 = s0;
    }
    return s0;
}

idea 3: DP with FSM

  • 一图胜千言: FSM

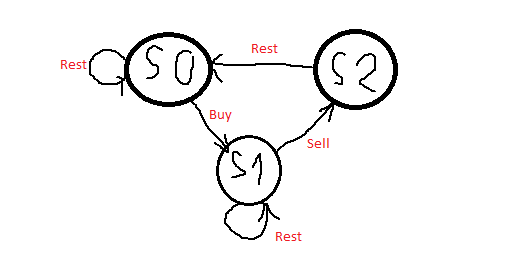
  • 发现这个post真是太赞了, 直接解决了BTBSS IV里面, 九章讲的不清不楚的. 这个图直接秒掉! 终于理解了

    • 通过循环引用的状态数组解决高级动态规划问题.
    • 通过FSM理解多个状态数组之间的关系!

  • 这里复习一下FSM, 在一开始各个state本身没有具体的定义, 而是之间的transit给出了具体的递推式子.

    • s0表示最初的状态, 它可以一直rest, 亦可以buy, 但不能sell(这是当然的, 必须buy之后才能sell).
    • s1表示buy了之后的状态, 可以接着若干次rest, 亦可以sell了.
    • s2表示sell了之后的状态. 此时必须rest(cooldown), 然后就能继续买卖了. 所以这个state就表示的cooldown.

  • 所以很容易得出递推公式:

    • s0[i] = max(s0[i-1], s2[i-1])
    • s1[i] = max(so[i-1]-prices[i], s1[i-1])
    • s2[i] = s1[i-1] + prices[i]

  • 那么各个state的INIT是什么呢?

    • s0[0] = 0. 第0天什么都不做.
    • s1[0] = -prices[0]. 第0天buy的话.
    • $$s2[0] = -\infty$$.
      • 无效状态, 因为必须buy了之后才能sell, 所以第0天就sell是不合法的. 参考背包九讲的初始状态的设计的tip.

  • 代码如下:

public int maxProfitFSM(int[] prices) {
    if (prices == null || prices.length < 2)  return 0;
    int[] s0 = new int[2];
    int[] s1 = new int[2];
    int[] s2 = new int[2];
    s0[0] = 0;
    s1[0] = -prices[0];
    s2[0] = Integer.MIN_VALUE;

    for (int i = 1; i < prices.length; ++i) {
      s0[i%2] = Math.max(s0[(i-1)%2], s2[(i-1)%2]);
      s1[i%2] = Math.max(s1[(i-1)%2], s0[(i-1)%2] - prices[i]);
      s2[i%2] = s1[(i-1)%2] + prices[i];
    }

    return Math.max(s0[(prices.length-1)%2], s2[(prices.length-1)%2]);
}