Rectangle Area

• Easy
• tag: math, 几何
• 类似题目: 多边形分三角, max colinear, KD-tree...

Find the total area covered by two rectilinear rectangles in a 2D plane.

• 题目给出左下和右上的坐标.

思路

• 一开始先看题目, 看有什么性质. 大概的思路就是: 2个面积之和, 减去, 重叠部分的面积.
• 不过这4个点给出来要分的情况很多, 怎么做? 有什么简单的方法吗?

idea:

• 看一下草图: .
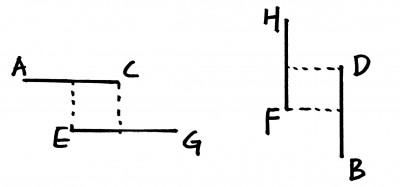• 可以不用先分类, 而是直接写出"重叠部分"的点, 然后再分类即可(?)
• 如上图所示, 其中虚线部分即是overlap的部分.
  • left = max(A,E)
  • right = min(C,G)
  • top = min(H,D)
  • bottom = max(B,F)

• 写出点后, 再分类就很容易了: 要想overlap部分有效, 即需要: right > left && top > bottom. 这比起通过2个大矩形判断重叠部分要简单太多了!

• 然后代码就很好写了, 这里参考的discuss的好解法.

public int computeArea(int A, int B, int C, int D, int E, int F, int G, int H) {
    //if (A <= C && C <= B && B <= D || C <= A && A <= D && D <= B) {
    //  if (E <= G && G <= F && F <= H || G <= E && E <= H && H <= F) {
    //    return Math.abs()  // 怎么分类???
    //  }
    //}

    int areaABCD = (C-A) * (D-B);
    int areaEFGH = (G-E) * (H-F);
    int left = Math.max(A,E);
    int right = Math.min(C,G);
    int top = Math.min(D,H);
    int bottom = Math.max(B,F);

    int ovlap = 0;
    if (right > left && top > bottom) {
      ovlap = (right - left) * (top - bottom);
    }

    return areaABCD + areaEFGH - ovlap;
  }

写后感

• 这里的难点是怎么判断有没有overlap. 我一开始是正向思维: 即通过2个矩形的坐标来判断, 但是分类很多, 很容易错乱.
• 实际上应该像find median那样: 可以求一般情况: find Kth Largest (Quick select: O(N)), 然后就很容易做了.
• 同样, 这里直接先假设有overlap, 求出left/right/top/bottom. 然后就超级容易判断是否存在了.
• 这种通过直接求解, 再判断的思维方式很重要!
• 还有一开始我总是混淆row/col, 以及x/y. 搞的坐标错乱, 而且居然忘了坐标轴的方向了... 搞错了max还是min.