Verify Preorder Sequence in Binary Search Tree

Medium
keyword: 单调栈
类似: Max Tree, Largest Rectangle

Given an array of numbers, verify whether it is the correct preorder traversal sequence of a binary search tree. You may assume each number in the sequence is unique.

idea1

考虑到BST的性质: 左儿子比自己小, 右儿子比自己大. 以及pre-order是: root-left-right.
举个例子:
```
        10
      /    \
     5      12
    / \     /
   2   7   11
      / \
     6   8
```
如上图所示:
- 对于preorder: [10,5,2,7,6,8,12,11]
- 对于inorder: [2,5,6,7,8,10,11,12]
可以看到: 在pre-order遍历的时候, 遍历右子树的时候, 所有值都比该右子树的父亲节点大. 例如: 走到5, 然后traverse 2左子树的部分都是小于5, 接着走7这个子树的所有值都要比5大. 所以具有单调性, 于是就想到了stack. 同时在左子树走完后走右子树前, 保存root, 作为有效性的判断, 因为右子树所有的值都要大于root.
代码如下: 这里和算法有点区别, 这里正好pre-order给pop出来的顺序是递增, 即inorder. 所以inorder的peek即low bound.

public boolean verifyPreorder(int[] preorder) {
    Stack<Integer> stk = new Stack<>();
    Stack<Integer> inorder = new Stack<>();
    for (int p : preorder) {
      if (!inorder.isEmpty() && p < inorder.peek()) {
        return false;
      }
      while (!stk.isEmpty() && p > stk.peek()) {
        inorder.push(stk.pop());
      }
      stk.push(p);
    }
    return true;
  }

验证一下上面的algs:
- stk: 10->10 5 -> 10 5 2 -> 10 7 -> 10 7 6 -> 10 8 -> 12 -> 12 11.
- inorder: null -> null -> null -> 2 5 -> 2 5 -> 2 5 6 -> 2 5 6 7 -> 2 5 6 7 8 -> 2 5 6 7 8 10.

follow up: 验证post-order

先复习一下怎么traverse:
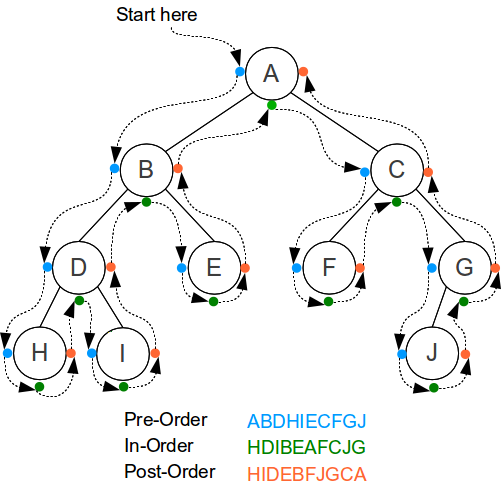
和preorder的区别在哪呢?
- preorder是: root->left->right. {10, 5, 2, 7, 6, 8, 12, 11}
- postorder是: left->right->root. {2, 6, 8, 7, 5, 11, 12, 10}
Inspired by : Ethan Li的SegmentFault题解. 代码如下:

public boolean verifyPostorder(int[] postorder) {
    int ub = Integer.MAX_VALUE;
    Stack<Integer> stk = new Stack<>();
    for (int j = postorder.length - 1; j >= 0; j--) {  // 注意是反过来遍历: left<-right<-root
      if (postorder[j] > ub) return false;
      while (!stk.isEmpty() && postorder[j] < stk.peek()) {
        ub = stk.pop(); // 也可以push到inorder stack里面
      }
      stk.push(postorder[j]);
    }
    return true;
  }