successor and predecessor in BST
- Medium
- keyword: recursion, stack
- 类似: BST LCA
Given a binary search tree and a node in it, find the in-order successor of that node in the BST. Note: If the given node has no in-order successor in the tree, return null.
思路:
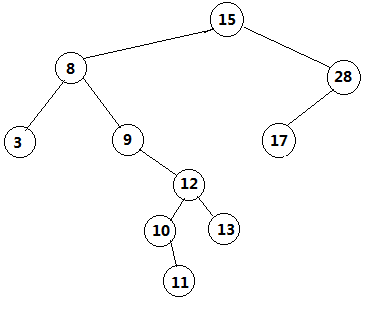
举个例子: 如下图
sucessor:
- 9的successor是10, 即9的右子树的最小值, 所以是left-most(并不一定是leaf!), 所以是10.
- 13的successor是15, 即15因为没有右子树, 所以大于他的node不在下面, 而在ancestors. 所以要找到第一个大于他的ancestor.
- 28的sucessor是null, 因为没有比他大的node了.
predecessor:
- 各自的predecessor也一样, 但是反过来.
- 9的predecessor是8, 即小于他的第一个数, 因为没有左子树, 所以向上找.
- 12的predecessor是11, 因为他有左子树, 所以找左子树里面最大的, 即先向左, 然后一直找右儿子. 有点像BST remove a node.
解法1: 直接实现算法(这里写sucessor的. predecessor同理)
通过上面的例子分析得到算法:
- 若p有右子树, 那么return右子树里面最小的node.
- 若p没有右子树, 则向上回溯知道root, 找比p大的第一个ancestor.
通过iteration可以解决, 代码如下:
public TreeNode inorderSuccessorLoop(TreeNode root, TreeNode p) {
Stack<TreeNode> path = new Stack<>();
TreeNode curr = root;
while (curr.val != p.val) { // 先定位p
path.push(curr);
if (curr.val < p.val) {
curr = curr.right;
}
else {
curr = curr.left;
}
}
if (curr.right != null) { // case 1: 有右子树. 找子树里最小的
curr = curr.right;
while (curr.left != null) {
curr = curr.left;
}
return curr;
}
else { // case 2: 没有右子树, 则通过刚才遍历的path, 一个个pop直到第一个比他大的node.
while (!path.isEmpty() && path.peek().val < curr.val) {
path.pop();
}
return path.isEmpty() ? null : path.pop();
}
}
解法2
- 由于递归自然是从top开始, 所以向下递归的时候, 自动保留了比他大的root(?). 这就要好好设计recursion了.
这里的要点在于: 向下搜索p的时候是:
- root<=p, 则向右递归(注意这里等于也是向右, 因为找比他大的第一个数).
- root>p, 则向左递归.
- 向左递归的时候, 因为root>p, 所以有可能是第一个比p大的ancestor. 所以这个时候返回的要和root比较. 那么什么时候比较呢: 当递归下去没有结果, 返回了null的时候.
这个recursion设计的很巧妙, 要细细领会.
- 代码如下:
public TreeNode successor(TreeNode root, TreeNode p) {
if (root == null)
return null;
if (root.val <= p.val) {
return successor(root.right, p);
} else {
TreeNode left = successor(root.left, p);
return (left != null) ? left : root;
}
}
- 可以通过找: 12, 20的successor来理解这个recursion.